Suppose you had $100 in a savings account and the interest rate is 20% per year and you never withdraw money or interest payments. After 5 years, how much would you have on this account in total?
- More than $200
- Exactly $200
- Less than $200
- Don’t Know
According to a survey of Americans between the ages of 40 and 60, by economists Annamaria Lusardi of George Washington University and Olivia S. Mitchell of the Wharton School of the University of Pennsylvania, 24.3% were unable to respond with the correct answer to this question. Regarding the respondents, over half of those surveyed had college or more years of education and nearly 30% earned at least $100,000 per year.
Financial literacy is an important skill to have when saving for retirement. The hypothetical question above addresses a fundamental component of savings; compound interest.
A mental shortcut to answering the question, that might tempt you to answer “exactly $200”, is to say that 20% of $100 is $20. Multiply $20 by five years, add the original $100 and arrive at exactly $200 at the end of the fifth year. But that answer is incorrect.
Due to the effect of compounding, interest earned also earns interest, therefore the correct answer is “more than $200”.
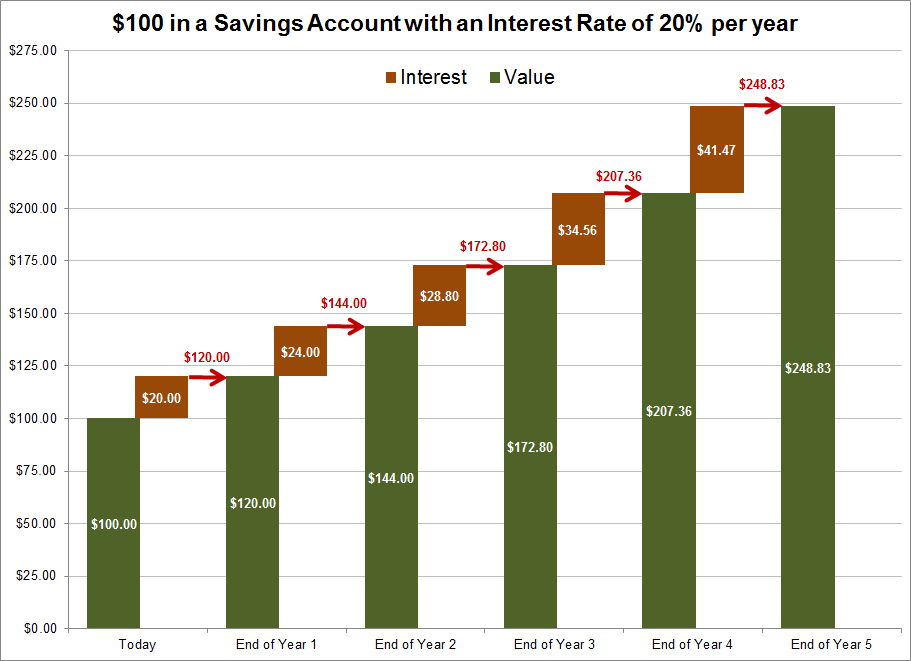
Here is how:
Today: $100.00
Year 1
- First Years Interest: $100 times 20% = $20.00
- End of Year 1: $100.00 + $20.00 = $120.00
Year 2
- Second Years Interest: $120 times 20% = $24.00
- End of Year 2: $120.00 + $24.00 = $144.00
Year 3
- Third Years Interest: $144.00 times 20% = $28.80
- End of Year 3: $144.00 + $28.80 = $172.80
Year 4
- Fourth Years Interest: $172.80 times 20% = $34.56
- End of Year 4: $172.80 + $34.56 = $207.36
Year 5
- Fifth Years Interest: $207.36 times 20% = $41.47
- End of Year 5: $207.36 + $41.47 = $248.83
Mathematically this can be calculated quickly by $100 * (1.20)^5 = $248.83.
Compound interest, a fundamental component of finance, works in the same fashion when you borrow. After all, the other side of the example above is the hypothetical bank. It has borrowed $100 from the individual and, if no money or interest payments are withdrawn ends up paying the person $248.83 at the end of year five.
Understanding the effect compound interest has, whether you are saving or borrowing, is an important concept to grasp for your long term financial well being.